SOEN 321

SOEN 321 Winter 2019

Outline

• Instructor: Dr. Mohammad Mannan
• Outline

Final

• Set 3: Stream cipher
• Set 4: Block cipher
• Set 5: Hash
• Set 6: MAC
• Set 7: PKI-SSL
• Set 8: Usability
• Set 9: Botnets-DDos
• Set 14: Inuksuk

Cheatsheet

Name	Block size	Key size	Output size	Rounds
DES	64	56		16
AES-128	128	128		10
AES-192	128	192		12
AES-256	128	256		14
SHA1			160
SHA2-256			256

---

0. Preparation

0.1 Modulus

$a\equiv b\pmod n$

• implies: $n$ divides $(a-b)$
• implies: $a\pmod n = b\pmod n$
• e.g.: $7\equiv 4\pmod 3$, $-11\equiv 17\pmod 7$

0.2 Pseudo-Random Number Generators (PRNG)

• Definition
  • A given PRNG is a deterministic function that takes a fixed-length key (seed) and produces anunbounded bit stream.
• Same seed (entropy source), same sequence
  • Hardware vs. Software sources
  • Sound/video input, disk drives
  • Elapsed time between emission of particles during radioactive decay
  • Linux (/dev/random)
  • Mouse, keyboard activities
  • Disk I/O
  • Interrupts
  • Embedded devices / IoTs
  • CPU support
  • Online service (should note be trusted)
• Produces “statistically random” numbers
  • it passes standard tests for randomness
• Cryptographically secure, if
  • Unpredictable (next-bit test): computationally infeasible to predict the next bit given a complete history of past bits.
  • Balanced: The number of $1$’s and $0$’s should be equal.

0.3 Some Other Types of Security

• Unconditional security:

  • The uncertainty in the plaintext, after observing the ciphertext, must be equal to the a priori uncertainty about the plaintext. Observation of the ciphertext provides no information to an adversary.

• Computational security:

  • level of computation required to defeat it (using best attack known) >> the computational resources of the adversary.
  • Data complexity is $2^n$: $n$ is the block size.
  • Processing complexity is $2^k$: $k$ is the key size.

0.4 Attack analysis

• Complexity of an attack
  1. Data complexity– expected number of required input data units (ciphertext blocks).
     • For a block of size $n$, it is $2^n$.
  2. Storage complexity – expected number of required storage units..
  3. Processing complexity – expected number of required operations on data.
     • For a key of size $k$, it is $2^k$.
• How to reduce complexity
  • possible parallelization

---

1. Trusting trust

1.1 Security stack

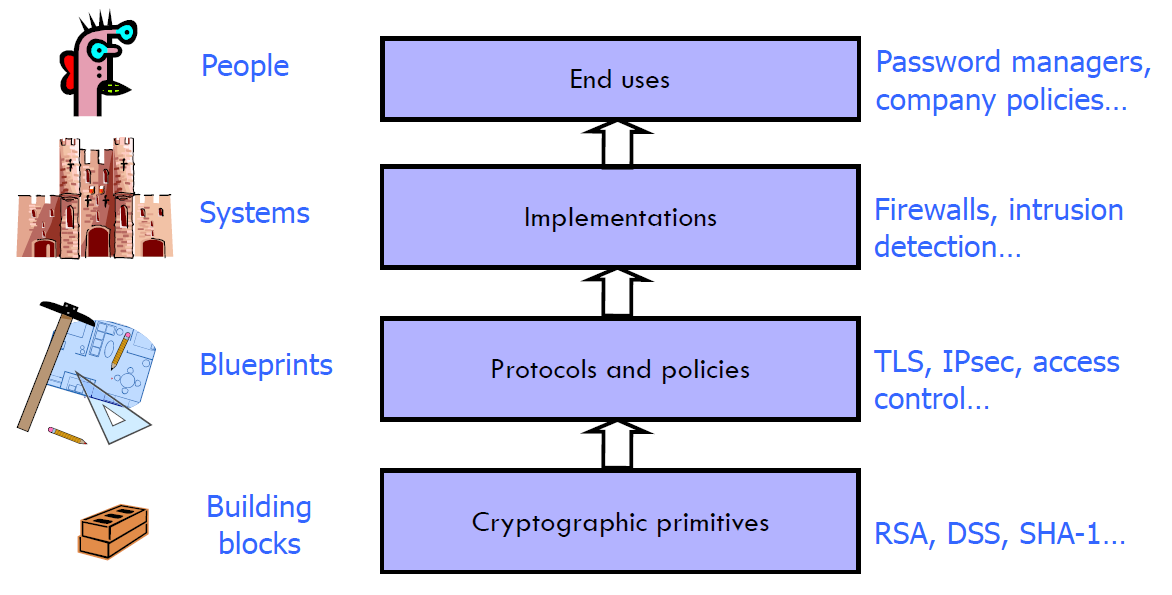
1.2 Security v.s. Correctness

• System security: System properties preserved in the face of an attack.
• System correctness: For reasonable input, get reasonable output.

1.3 What code to trust?

1. Is Windows/OSX binary reliable?
2. No. So we use open-source, or wirte our own.
3. But we need to compile.
4. Who wrote the compiler?
5. So inspect the source code of the compiler, and recompiler the compiler.
6. But there is another compiler.

   "The moral is obvious. You can't trust code that you did not totally create yourself."

1.4 Examples

• The Bullrun project
• The PRISM Program

1.5 Security Mindset

“Think like an attacker, but do not attack.”

---

2. Cryptography

Cryptography $\neq$ Security

2.1 What Cryptography is

Cryptography is the study of mathematical techniques related to aspects of information security such as confidentiality, data integrity, entity authentication, and data origin authentication.

• Always think from three perspectives
  1. Defenders' view point
  2. Attackers' view point
  3. How much it will cost – to protect & to attack

2.2 What Cryptography for

1. Confidentiality: prevent others from reading a message
2. Integrity: someone didn’t replace or modify a message
3. Data origin authentication: a message originated from a certain source
4. Entity authentication: a person is who he/she claims to be. e.g.: password
5. Non-repudiation: prevent someone from denying past commitments or actions; that is, someone cannot deny the validity of something.

2.3 Cryptology

• Cryptology = Cryptography + Cryptanalysis
• Cryptanalysis: Study of code breaking

2.4 Basic tools of cryptography: Security Primitives

1. Unkeyed Primitives
   • Hash functions
   • One-way permutations
   • Random sequences
2. Symmetric-key Primitives
   • Symmetric-key ciphers
     • Block ciphers
     • Stream ciphers
   • Message Authentications Codes (MACs)
   • Signatures
   • Pseudorandom sequences
   • Identification primitives
3. Public-key Primitives
   • Public-key ciphers
   • Signatures
   • Identification primitives

2.5 Attacker model

1. Passive vs. active attacker
2. What computational resources the attacker has?
3. What does the attacker know about a system?
4. What are the assumptions?
   • encryption keys are shared via a secure channel

2.6 Encryption

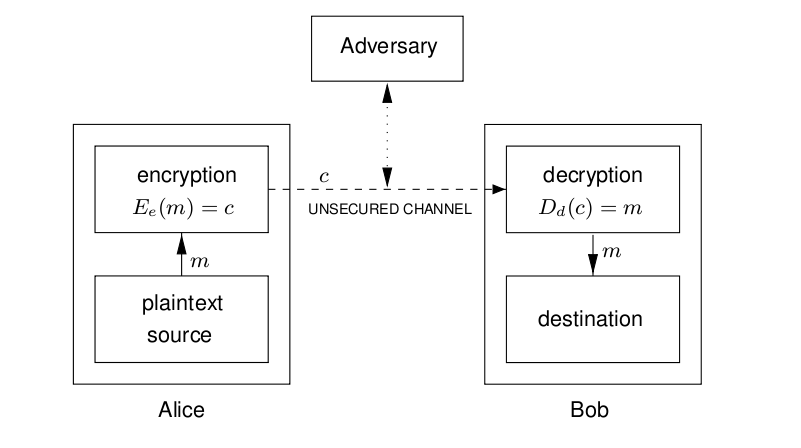
• Goals
  1. Data confidentiality
  2. Protect a large amount of data with "short" secrets, like a lock-and-key.
  3. Make it difficult for those without the secret key; efficient retrieval with the correct key.
• Simple model
  • What to hide: key + plaintext
• Terminologies
  1. plaintext - the original message, denoted $m$ or $p$
  2. ciphertext - the encoded message, denoted $c$
  3. cipher - algorithms for transforming plaintext to ciphertext and vice-versa
  4. key - info used in cipher known only to sender/receiver
  5. encipher (encrypt) - converting plaintext to ciphertext, denoted $E()$
  6. decipher (decrypt) - recovering ciphertext from plaintext, denoted $D()$
  7. substitution – each element is mapped into another
  8. transposition – rearrangement of elements
• Kerckhoff’s Principle
  • Security should depend only on the key
    • Don’t assume enemy won’t know algorithm
    • Can capture machines, disassemble programs
    • Too expensive to invent new algorithm if it is compromised
  • Security by obscurity does not work
• History
  • Classical ciphers
    • Pen & paper, simple mechanical machines
    • Egyptians, Greeks, Romans, Hebrew scholars
  • World War I
    • Vernam Cipher (one time pad)
  • World War II
    • Complex electro-mechanical machines
    • Enigma
  • Modern crypto
    • Depends on – computers, math
    • Data Encryption Standard (DES) – 1975
    • Public key systems – 1976
    • Common people use

2.7 Examples

1. Substitution ciphers

• How it works
  • Each symbol in plaintext is replaced by another symbol according to some fixed permutation
    • e.g.: Repalce $A$ by $D$, $B$ by $G$.
  • For a set of English characters, all possible mappings is $26!$.
  • But such a large key space does not mean it is secure (why? Pattern).
• Substitution is said to add confusion (makes relationship between key and ciphertext as complex as possible)
• Break it: Brute force key search
  • English letter frequencies

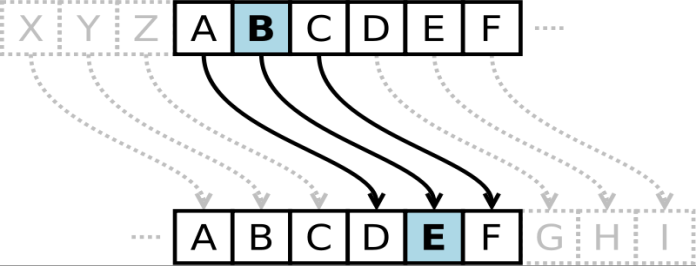
Shift/Caesar cipher

• How it works
  • It is one type of simple substitution cipher.
  • Shift each letter by an offset.
  • For a set of English characters, all possible mappings is $25$.
• Break it: Brute force
  • Only $25$ keys

Polyalphabetic substitution

• How it works
  • Multiple substitution alphabets
    • Vigenère cipher
    • Enigma
  • Pick a keyword, repeat it to mapping plaintext.
  • Lookup in the table using the keyword letter and its conresponding plaintext letter.
• Transposition is said to add diffusion (spreading out bits so redundancy in plaintext is spread over ciphertext), so more resistant to frequency analysis.
• Break it

Transposition cipher

• How it works
  • With a fixed period $t$,
  • grouping the plaintext into blocks of $t$ characters,
  • applying to each block a single permutation $e$ on the numbers $1$ to $t$.
• e.g.: $t=6$
  • $m=CAESAR$
  • $e=(6\ 4\ 1\ 3\ 5\ 2)$
  • $c=RSCEAA$
  • $d=(3\ 6\ 4\ 2\ 5\ 1)$

2. Block & stream ciphers

Block cipher

• plaintext message is broken into fixed-length blocks before encryption
• one block is processed at a time
• most modern ciphers are block ciphers

Stream cipher

• block length is one
• requires only limited buffering of data

2.8 How to attack encryption

1. Cryptanalysis
   • Search for weaknesses in the algorithms
   • (Partial) knowledge about plaintext, ciphertext
2. Brute-force
   • Try all possible keys ($N$)
   • On average $N/2$ trails are required
3. Malware, key/screenlogger, physical and side-channel attacks...

Attacks on encryption schemes

1. Ciphertext-only attack - deduce the decryption key or plaintext by only observing ciphertext
2. Known-plaintext attack - using a quantity of plaintext and corresponding ciphertext
3. Chosen-plaintext attack - choose plaintext and is then given corresponding ciphertext
4. Adaptive chosen-plaintext attack - chosen-plaintext attack where the choice of plaintext may depend on the ciphertext received from previous requests
5. Chosen-ciphertext attack - select the ciphertext, then the corresponding plaintext is given
6. Adaptive chosen-ciphertext attack - chosenciphertext attack where the choice of ciphertext may depend on the plaintext received from previous requests

---

3. Stream ciphers

• Synchronous stream ciphers
  • Key-stream is generated independently of plaintext and of ciphertext
• Self-synchronizing stream ciphers
  • Key-stream is generated as a function of the key and a fixed number of previous ciphertext digits
• Examples:
  • Vernam cipher
  • One-time pad
  • RC4
  • ChaCha20

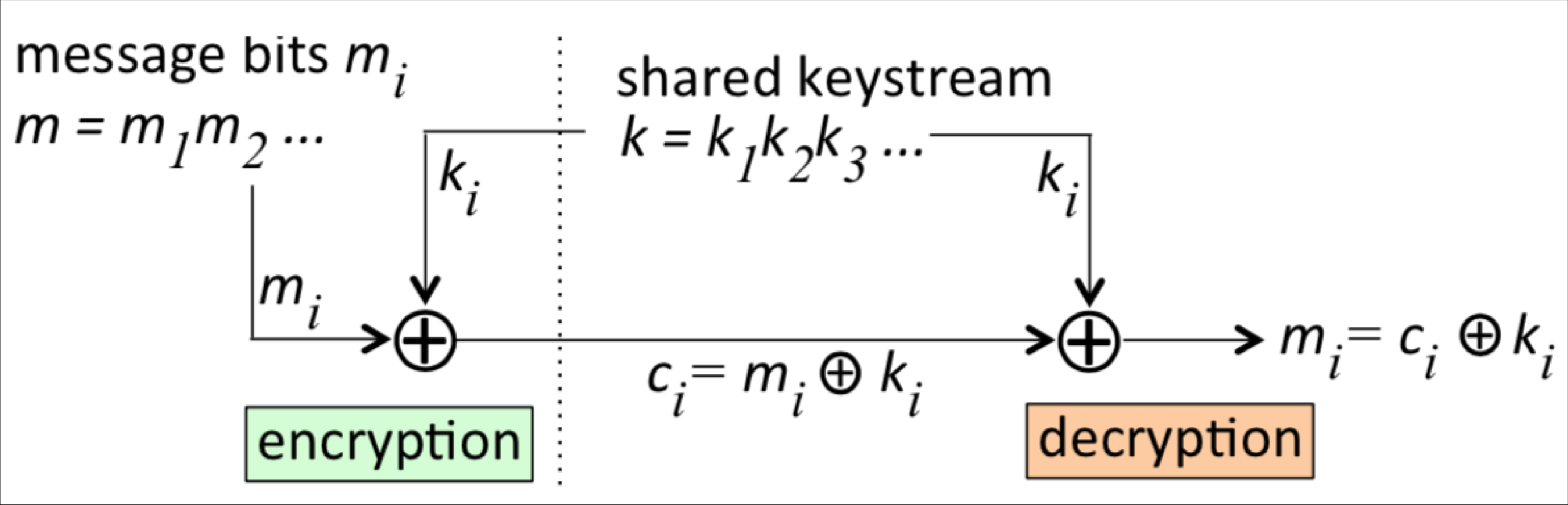
3.1 Vernam Cipher

• How it works
  • Plaintext: $m_1m_2\ldots m_t$
  • Key string: $k_1k_2\ldots k_t$
  • Cipertext: $c_1c_2\ldots c_t$
  • $c_i=m_i\oplus k_i, 1\leq i\leq t$

3.2 One-time pad

• Why we need it

  • Vernam cipher "can" use any bit source as a keystream,
  • But for real security the key should be random and never use again.
  • Vernam cipher with such a key-stream is called a one-time pad.
  • The one-time pad is provably secure.
  • One-time pad is unconditionally secure against a ciphertext-only attack, observation of the ciphertext provides no information to an adversary.

• How it works

  • Same as vernam cipher

• What if

  • Reuse the key-steam

    • If ciphertexts and one plaintext are known.

      $\begin{aligned} &\text{Ciphertext}_1\oplus\text{Ciphertext}_2\\ =\ &\text{Plaintext}_1\oplus\text{key}\oplus\text{Plaintext}_2\oplus\text{key}\\ =\ &\text{Plaintext}_1\oplus\text{Plaintext}_2 \end{aligned}$

  • Not random

    • Brute-force

• Probability of $0$ and $1$ in ciphertext

  • In the plaintext, assume the probability $p(0)=x$, then $p(1)=1-x$.
  • Assume the probability of a key bit $p(0)=p(1)=1/2$.
  • Four cases:
  1. $p(m_i=0,k_i=0)=x\cdot 1/2=x/2$
  2. $p(m_i=0,k_i=1)=x\cdot 1/2=x/2$
  3. $p(m_i=1,k_i=0)=(1-x)\cdot 1/2=(1-x)/2$
  4. $p(m_i=1,k_i=1)=(1-x)\cdot 1/2=(1-x)/2$
  • So:
    • $p(c_i=0)=p(c_i=1)=x/2+(1-x)/2=1/2$
  • But:
    • No integrity

3.3 RC4

• What it is
  • Byte-oriented, fast in software
  • Variable-length key: 40 – 2048 bits
  • Similar to the one-time pad except that generated pseudorandom bits, rather than a prepared stream, are used.
• How it works
  • Initialization: the permutation $S$ is initialized with a variable length key.
  • Keystream: the stream of bits is generated using $S$ and two 8-bit index-pointers (denoted $i$ and $j$).
  • $\oplus$, same as one-time pad.

3.4 ChaCha20 stream cipher

• What it is
  • 256-bit key
  • 96-bit nonce
  • 32-bit block counter
• How it works
  • Output a 64-byte block of key stream and increments block counter in each invocation
    • $k=\text{chacha{\textunderscore}stream(key, nonce, counter)}$
  • $c_i = m_i \oplus k_i$
  • If never use the same nonce with the same key twice, it is a one time pad.

---

4. Block ciphers (symmetric key)

• What it is
  • A function that maps $n$-bit plaintext blocks to $n$-bit (blocklength) ciphertext blocks.
  • If key $K$ is $k$ bits long, the number of keys is $2^k$.
  • Encryption: $C = E(M,K)$
  • Decryption: $M = D(C,K)$
  • The encryption function $E_k$ must be one-to-one (bijection).
    • One-to-one: Because the encryption and decryption process must be reversed.
    • Not onto: Some $c_i$s have no correspoing $m_i$s, so if a bit flip occurs, decryption would fail.
    • Not one-to-one: Ambiguity, $c_i$ maps more than one $m_i$.

• Used for
  1. Data confidentiality
  2. MACs
  3. PRNGs (pseudorandom number generators)
  4. Authentication
• Very efficient software and hardware implementations
  • Can be used in low-resource devices
• Practical security
  • Standard assumptions (in addition to Kerckhoff's):
    • attacker has access to all transmitted ciphertext.
  • A block cipher is:
    • totally broken if key is recoverable, and
    • partially broken if (some) plaintext is recoverable (without a key)
• Modes of operation
  • How to employ block ciphers for large messages
    1. Dividing messages
    2. Padding the last block
  • Basic modes
    • ECB: Electronic Code Book
    • CBC: Cipher Block Chaining
    • OFB
    • CFB
  • Initialization Vector (IV)
    • A block of data used in addition to the input message
    • Randomize the encryption process

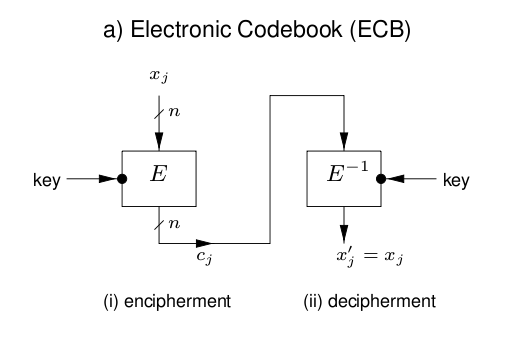
4.1 Electronic Codebook (ECB)

• Overview
  • Same plaintext result in identical ciphertext
  • Blocks are enciphered independently of other blocks
  • Bit errors in a single ciphertext affect decipherment of that block only
• How to
  • $c_j=E_k(x_j)$
  • $x_j=E^{-1}(c_j)$

• Weakness
  • Does not hide data patterns
  • Malicious substition of ciphertext is possible

• Usage
  • When can we use this mode:
    • Plaintext that has size of less than one block, to avoid pattern
  • When not to use it:
    • Multi-block messages
    • Key are reused more than a single block

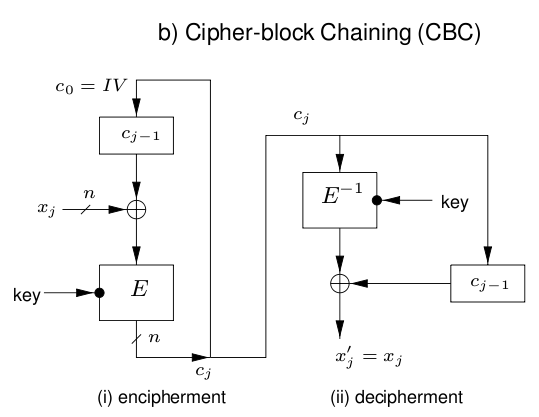
4.2 Cipher Block Chaining (CBC)

• Overview

  • Chaining causes ciphertext $c_j$ to depend on all preceding plaintext
  • Random access to encrypted data is not possible because of the previous reason.
  • Also because of that, only the same key, IV, plaintext results identical ciphertext.
  • IV must be integrity-proteced
    • If not, attackers may make predictable bit changes to the 1st block.
    • If your salary is saved as $0111010$, you can flip the $0$ in IV corresponding to $0$ in your salary to change your salary to $1111111$.
  • A single bit error in $c_j$ affects decryption of blocks $c_j, c_{j+1}$.

• How to

  • $c_j=E_k(c_{j-1}\oplus x_j)$ for $j\geq 1$, $c_0=IV$
  • $x_j=c_{j-1}\oplus E^{-1}(c_j)$ for $j\geq 1$, $c_0=IV$

• Weakness
  • Has known weaknesses?

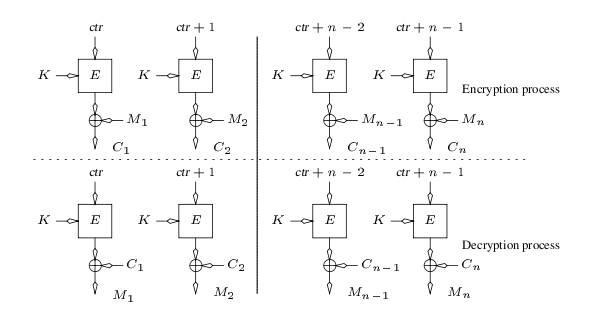
4.3 Counter mode (CTR)

• Overview

  • CTR must be different for each block
  • An IV/nonce value is also used with the counter for uniqueness (concat/addition/xor)

• Advantage:

  1. Software and hardware efficiency: different blocks can be encrypted in parallel
  2. Preprocessing: the encryption part can be done offline and when the message is known, just do the XOR.
  3. Random access: decryption of a block can be done in random order, very useful for hard-disk encryption.

• How to

4.4 XTS-AES

• XEX (xor-encrypt-xor): efficient processing of consecutive blocks within a data unit.
• CTS (CipherText Stealing): provides support for sectors with size not divisible by block size.
• XTS: XEX-based Tweaked CodeBook mode (TCB) with CipherText Stealing (CTS).

4.5 ECB-CTS

• How to

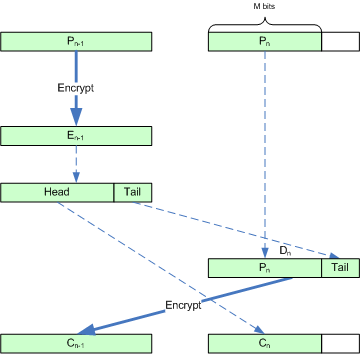
• Why //TODO

4.6 Block cipher: design components

Avalanche effect

• Slight change in input (e.g., flipping a single bit) significantly changes the output (e.g., half the output bits are flipped)
• Strongly desired property of:
  • Block ciphers
  • Cryptographic hash functions

Product cipher

• Execution of two or more simple ciphers in sequence (round of operations), such that the final product is cryptographically stronger than its components
• In particular, alternating substitutions and transpositions

Block cipher design approaches

• A round function is used
  • Strong avalanche effect
  • Bijective
• Repeated multiple times ($n$ rounds)
  • Round $1$ input: plaintext block
  • Round $n$ output: ciphertext block
  • Round key: derived fromthe key $K$, for each round
• Examples
  • SP networks (used in AES, CAST-128)
  • Feistel structures (used in DES, RC5, Blowfish)

Substitution-permutation (SP) network

• How to

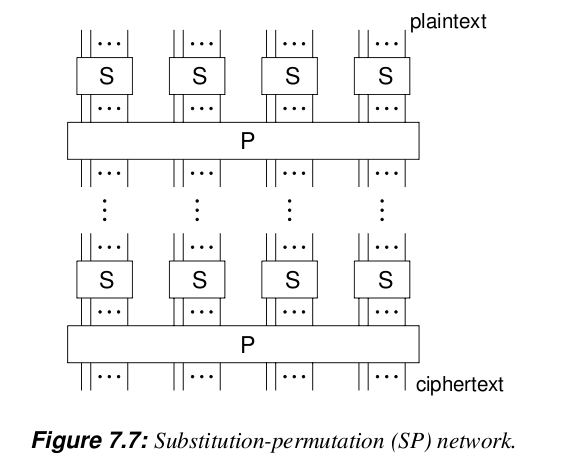
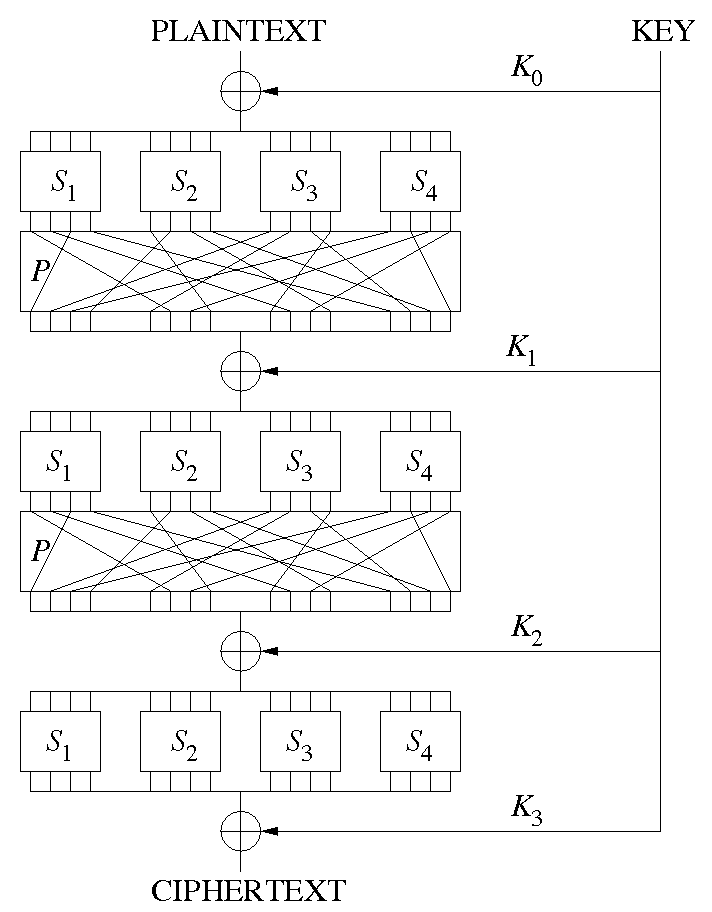
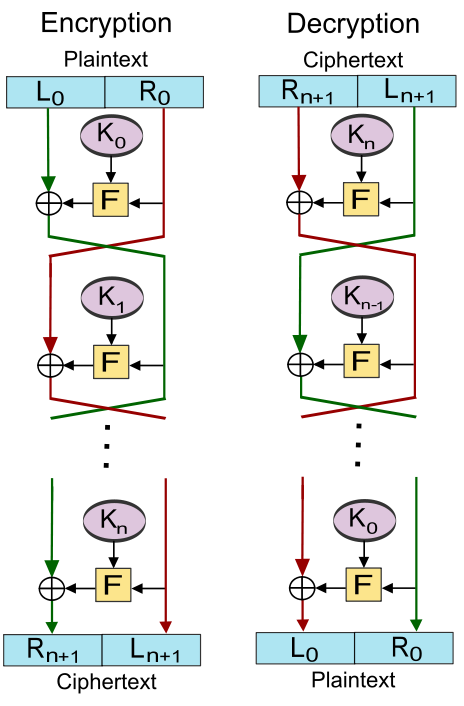
Feistel structure

• Overview

  1. Consists of a number of identical rounds of processing
  2. In each round, a substitution is performed on 1/2 of plaintext block, followed by a permutation that interchanges two halves
  3. The original key is expanded so a different key is used in each round
  4. The Data Encryption Standard (DES) exhibits this structure

• How to

  • $L_i = R_{i-1}$
  • $R_i=L_{i-1}\oplus f(R_{i-1},K_i)$

• Feistel structure parameters
  • Block size & key size:
    • larger means greater security, but may slow down encryption/decryption speed
  • Number of rounds:
    • more rounds means greater strength
    • typically 16 rounds
  • Subkey generation algorithm & round function:
    • greater complexity should lead to greater cryptanalysis resistance

4.7 Data Encryption Standard (DES)

• Overview
  • Use the Feistel structure
    • Block length $n=64$, key size $k=56$.
    • Number of rounds is $16$.
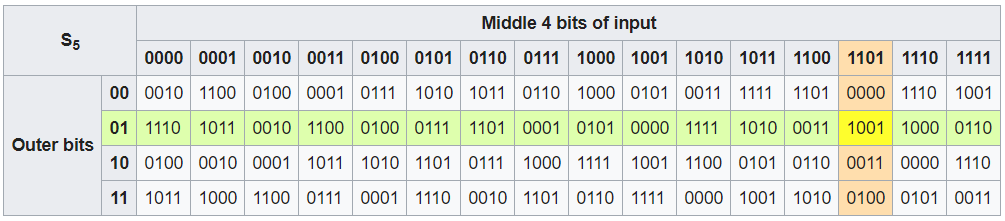
• S-box (substitution-box)
  • Outer bits: two bits (the first and last bits)
  • Inner bits: the other four bits between the first and last bits
  • e.g.: $011011$, outer bits are $01$, inner bits are $1101$.

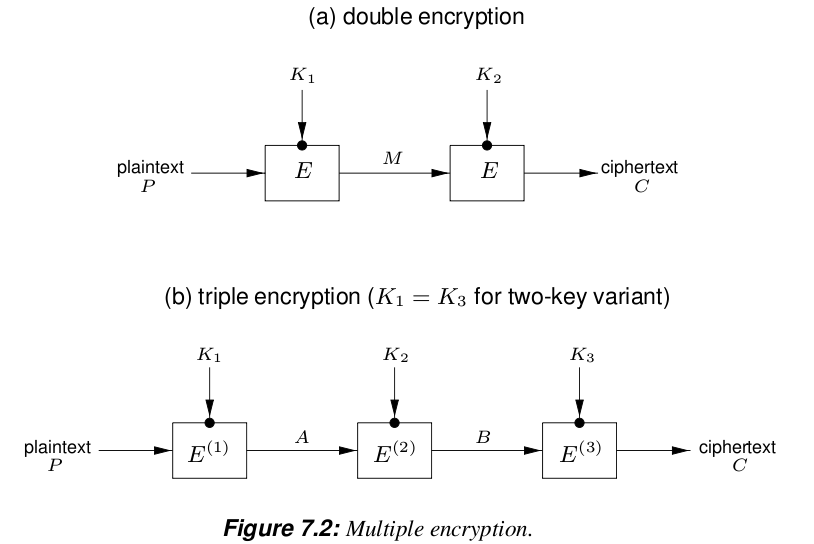
• Double/Triple encryption (DES)

  • The security of DES depends on its large key space.

  • Double encryption should double the size ($2^{112}$) of the key space?

  • $C=E_{k_2}(E_{k_1}(P))$

    

  • Meet-in-the-middle attack (DES)

    • Double-DES: $M=E_{k_1}(P)=D_{k_2}(C)$

      1. Compute and store $E_{K_1}(P)$ for all possible $K_1$
      2. Compute and store $D_{K_2}(C)$ for all possible $K_2$
      3. Match
      4. Reduces key search from $2^{2k}$ to $2^k$ at the expense of addition storage $2^k$.

    • Triple encryption: Security of $2^{112}$

• Alternative to DES

  • Double-DES - no security advantage
  • Triple-DES - secure, but slow
  • So, Advanced Encryption Standard (AES)

4.8 Advanced Encryptioin Standard (AES)

• Overview

  • Block length: $128$
    • Consider it as a $4\times4$ matrix of bytes: $4\times4=16\text{ bytes}, 16\times8=128\text{ bits}$
  • Key length: AES-128 (n=10), AES-192 (n=12), AES-256 (n=14)

• How to

  1. Derive round kyes (KeyExpansion): State = X(input)

  2. Initial round: AddRoundKey(State, $Key_0$): State $\oplus$ Expanded key

  3. Rounds (Nr-1 times)

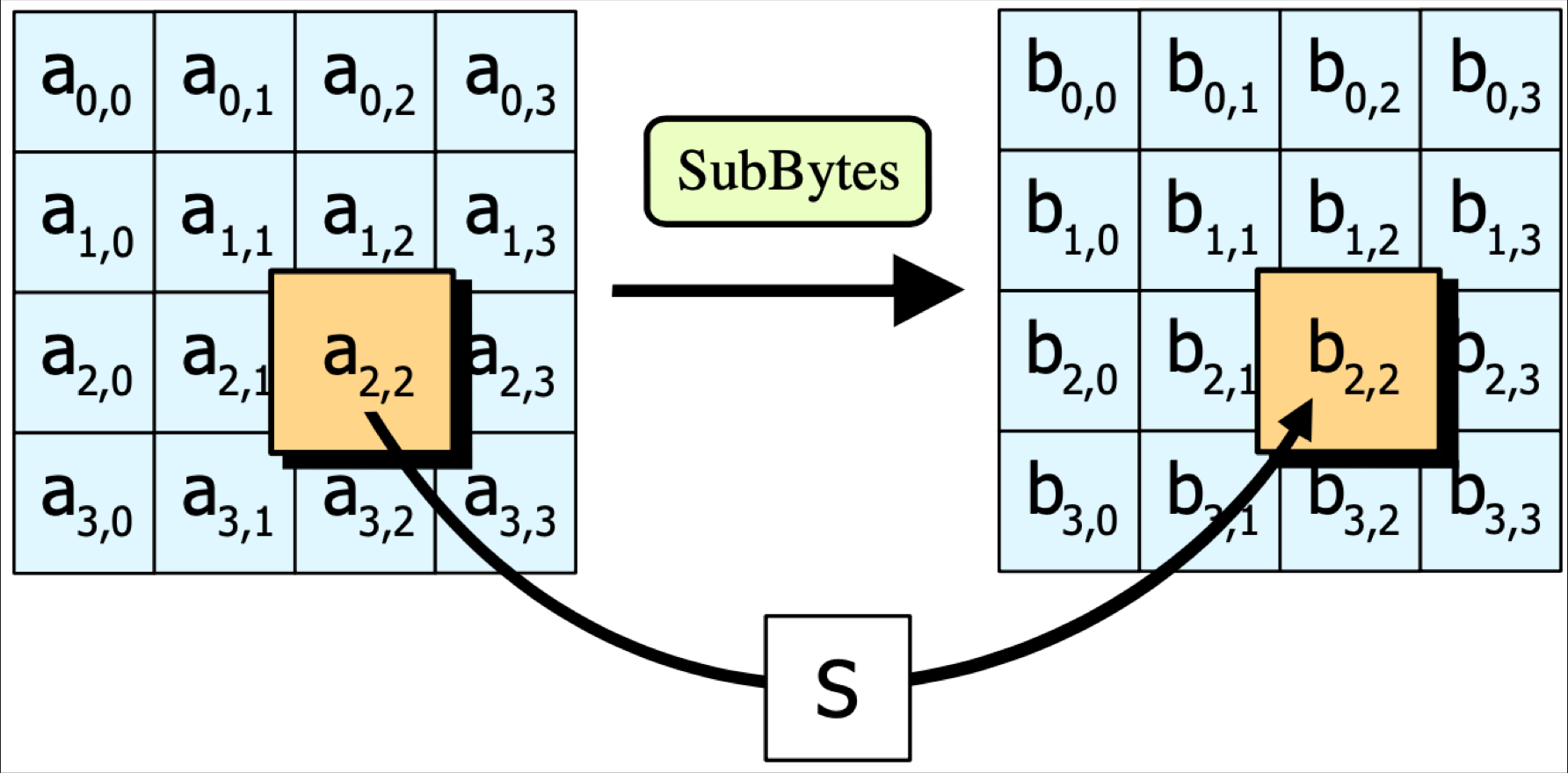
     1. SubBytes(State, S-box): a substitution step

        • Each byte in the state is replaced with its entry in a fixed 8-bit lookup table S (substitution box or S-box).
        • Provides non-linearity.

        

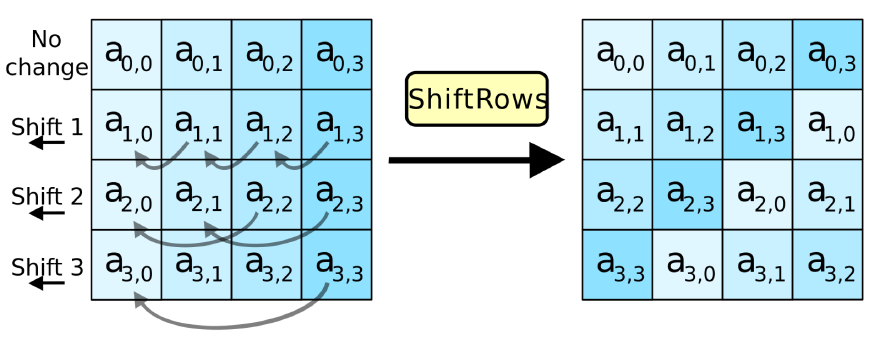
     2. ShiftRows(State): a transpositioin step

        • Avoid the columns being encrypted independently.

        

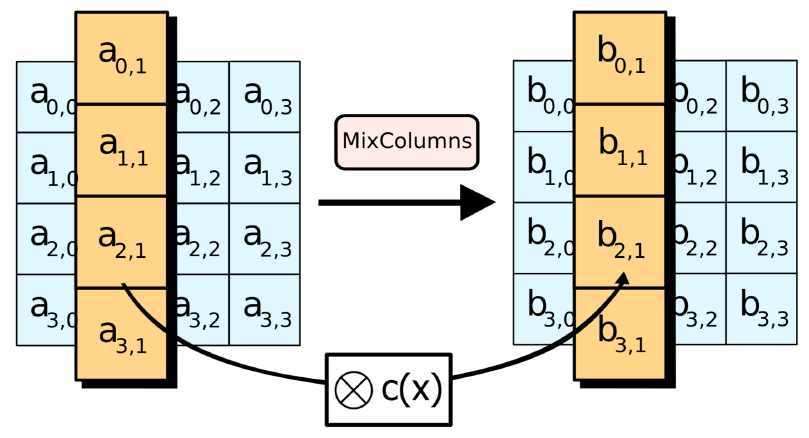
     3. MixColumns(State):

        • Each column of the state is multiplied with a fixed polynomial.
        • Together ShiftRows, MixColumns provides diffusion.

        

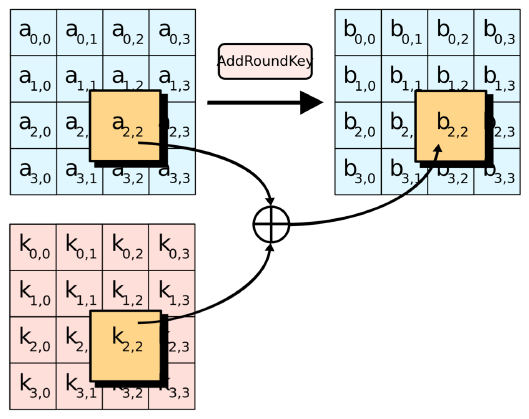
     4. AddRoundKey(State, $Key_R$):

        • The round subkey is combined with the state using bitwise XOR
        • For each round, a subkey is derived from the main key using Rijndael's key schedule

        

  4. Final Round (no MixColumns)

     1. SubBytes
     2. ShiftRows
     3. AddRoundKey

  5. Y(output) = State

• Attack

  • No practical attacks to date
  • No attacks on full AES versions

---

5. Hash Functions

5.1 What it is

• Input: a string $M$ of arbitrary length, called the preimage.
• Output: a string $h(M)$ of fixed length, called hash-value, hash-code, hash-result, or hash.
• Collsions: $h(M)$ is a many-to-one function
  • Assume $t$ to $n$, and $h$ is random.
  • $2^t$ input, $2^n$ output, so $2^{t-n}$ inputs would map to the same output.
  • Collisions probability: $1/2^{n}$
• Properties:
  1. Compression
  2. Ease of computation
  3. Pre-image resistance (one-way property)
     • Given $y$, to find any pre-image $x'$ such that $h(x')=y$.
     • But remember: there are no known provably one-way functions.
  4. Second pre-image resistance (Weak collision resistance)
     • Given $x$, to find a 2nd-preimage $x'$ where $x'\neq x$ such that $h(x')=h(x)$.
  5. Collision resistance (Strong collision resistance)
     • Find any $x', x$ where $x'\neq x$ such that $h(x')=h(x)$.
     • Need to guess $2^{n/2}$ inputs before finding a collision (birthday paradox).
• Examples:
  1. MD5: 128-bit hash
  2. SHA-1: 160-bit hash
  3. SHA-2 (SHA-256): 256/384/512-bit hash
  4. SHA-3
• Attack
  1. Dishonest signer
     • Signs $x_1$, later claims signed $x_2$ instead.
  2. Dishonest verifier
     • Gets signature on $x_1$, later claims signature on $x_2$.

5.2 Classification

• keyed
  • Message authentication (MACs)
  • Other applications
• Unkeyed
  • Modification detection (MDCs)
    • One-way hash function (OWHF)
      • Preimage and 2nd-preimage resistance
      • $n\geq128$
    • Collision resistant hash function (CRHF)
      • 2nd-preimage and collision resistance
      • $n\geq256$ because of birthday paradox ($2^{256/2}=2^{128}$).
        • Assumptions: $2^{128}$ operations are infeasible.
  • Other applications

5.3 How to build a hash function

1. Modular arithmetic
2. Block ciphers
3. Dedicated design

5.4 General structure of iterated Hash Functions

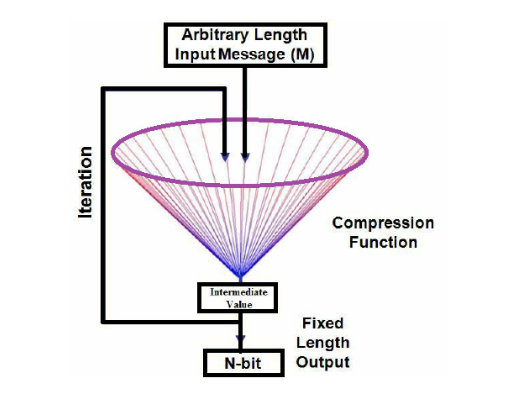
The Merkle–Damgård (MD) Construction of hash functions

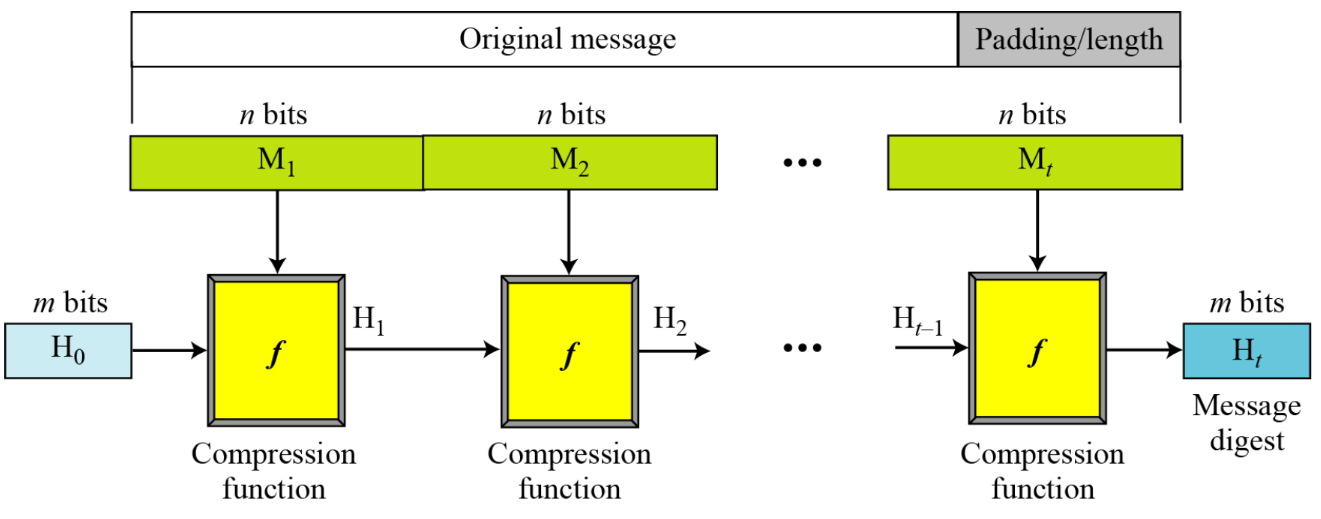
• How

  1. Padding, because compressions functions cannot handle inputs of arbitrary size.
  2. Divide into equal parts.
  3. $H_i=f(H_{i-1}, M_i)$

• Properties:

  • If $f$ is collision resistant, so is $h$.

5.5 Hash functions based on block ciphers

• Why
  • Trust
  • Reduce design, evaluation, and implementation effort
  • Compact implementation
• Why not
  • Slow
  • weaknesses which are not relevant to encryption
    • Block cipher could become weaken when used in $h()$.

5.6 Applications

• Data integrity
  • Messages
  • Files
• Confirmation of knowledge
  • Passwords
• PRBGs: Cryptographically secure pseudo-random bit sequences generator
  • Hash functions are designed to be “random functions” of the input.
  • Examples: /dev/random, /dev/urandom (Linux)
    • Acting as an entropy pool.
    • /dev/random blocks when no bits available, but /dev/urandom keeps going by SHA-1 (later by ChaCha20).
  • Seed
    • Avoid to use a simple value that an attacker could guess, e.g.:
      • System time
      • Process ID

5.7 Pre-computation attacks (Rainbow-table hash-chain attacks)

• How to
  • Pre-compute all hash values under given inputs, and only store some fraction to save space (space-time tradeoff) to optimize future search.
  • Variable-length messages do not generally have this problem, since input space is large
    • Example: passwords have a fixed size, rainbow-table can be applied.
• Protect against pre-computation: salts
  • Random value $s$ prepended to $p$ prior to calculating hash: $h(s\|\|p)$.
  • So an attacker would need to build a table for each possible salt value.

---

6. Message Authentication Code (MAC)

6.1 What it is

• Keyed hash functions are called MACs, which use both $M$ and a key $k$ as input.
• Why need it
  • Encryption alone does not provide data integrity.
• Goal
  • add authentication to the hash-value by using a secret (symmetric) key.
• Properties
  • Should be difficult to create a valid MAC without knowledge of secret key
• Usage
  • Message authentication: Alice sends $M \|\| h_k(M)$
  • Message authentication and confidentiality, where authentication is tied to:
    • Plaintext: $E_{k_2}(M\|\|h_{k_1}(M))$
    • Ciphertext: $E_{k_2}(M)\|\|h_{k_1}(E_{k_2}(M))$
  • Weakness: Does not provide non-repudiation

6.2 MDC vs MAC

• MDC should not be used for a MAC
• $MAC=h(k\|\|x)$: length-textension attack
  1. $h$ is an interated MDC with compression function $f$.
  2. $y$ is an attacker-controlled message.
  3. Attacker can computer $f(MAC,y)$ to obtain $MAC'=h(k\|\|x\|\|y)$ without knowing $k$.
• $MAC=h(x\|\|k)$: collision
  • Collision in the hash function will lead to a collision in the MAC.

6.3 Hash-based MAC

HMAC

• $HMAC(x)=h\big(k\|\|p_1\|\|h(k\|\|p_2\|\|x)\big)$
  • $k$ is the key $K$ padded with zeros on left so it has length of 1 block for compression function.
  • $p_1, p_2$ are distinct repeated byte strings of length $b$
  • $h$ any cryptographic hash function
• SHA-3 itself is immune to length extension attacks, so $MAC=SHA3(key\|\|message)$ would be sufficient.

6.4 MAC from block ciphers: CBC MAC

• Problematic if
  • Weak block cipher is used (e.g. DES)
  • Message length is variable

6.5 Password-Based Key Derivation Function (PBKDF2)

• $DK=PBKDF2(PRF,P,S,c,dkLen)$
  • $PRF$: hash or MAC function
  • $P$: Password
  • $S$: Salt value
  • $c$: Number of iterations
  • $dkLen$: required key length

---

7. Public Key Cryptography and SSL

7.1 Overview

• Why
  • In symmetric key systems, we have to share a secret key that nobody else knows.
  • Split this key into two pieces, one is public, the other is private.
• How
  • Uses number theoretic concepts: factoring, quadratic residue, RSA/DH problems
• It is asymmetric cryptography.
• Symmetric vs. public key Cryptography
  • Keys in symmetric cryptosystem
    • random bit strings
    • no special mathematical properties
    • generation is relatively easy
  • Keys in asymmetric cryptosystem
    • have speical mathematical properties
    • generation is computationally expensive
  • Key sizes are not comparable
    • RSA-1024
    • AES-128
    • But still AES-128 is better
• Advantages
  • Only private key must be secret
    • Still, authenticity of public key must be guaranteed.
  • The number of keys required is smaller than if symmetric keys used in large networks.
    • Symmetric: Every pair of 2 people need a different key, $\binom{n}{2}=n(n-1)/2\in O(n^2)$
    • Public key system: Every one has a key pair: $2n\in O(n)$
• Disadvantages
  • Speed: Encryption is much slower than symmetric ciphers.
  • Key sizes are typically much larger
  • No public key cipher proven to be secure (although the same can be said for block ciphers)

7.2 Public Key Cryptography

• Uses two different keys: one publie $K_e$, the other private $K_d$
  1. Alice generate $K_d$ only known to her.
  2. Alice generate $K_e$ which she publishes, avaliable to both Bob and Oscar.
  3. Knowledge of $K_e$ does not reveal $K_d$, or even given an advantage to Oscar trying to find $K_d$.
  4. Alternatvie notation for Alice's keys: $K_A, {K_A}^{-1}$.
• Theory: trapdoor one-way function
  • A function $f:\\\{0,1\\\}^* \rightarrow \\\{0,1\\\}^*$ is a trapdoor one-way function if and only if $f(x)$ is a one-way function.
  • Given some extra information, it becomes feasible to compute $f^{-1}$.
  • Public key cyrptography relies on trapdoor one-way function.
• Applications
  • Encryption: let anayone send you a message that only you can read.
  • Signature: let anyone verify that a message is from you.

7.3 Public Key Encryption

• Public-Private Key Pairs Properties
  1. Should be infeasible to find decryption key given encryption key and algorithm.
  2. Public key schemes utilise problems that are easy (P type) in one way but hard (NP type) in the other way, eg:
     • Exponentiation vs. logs
     • Multiplication vs. factoring
• How
  1. Alice wants to send a message $M$ to Bob. She knows his public key $K_{e,Bob}$ since it is public.
  2. Alice encrypts $M$ using $K_{e,Bob}$ producing $C$.
  3. Bob decrypts $C$ using $K_{d,Bob}$, a private key generated by Bob that corresponds to $K_{e,Bob}$.
     • Only $K_{d,Bob}$ can decrypt a message encrypted with $K_{e,Bob}$.
     • Notice this means that even Alice cannot decrypt $C$.

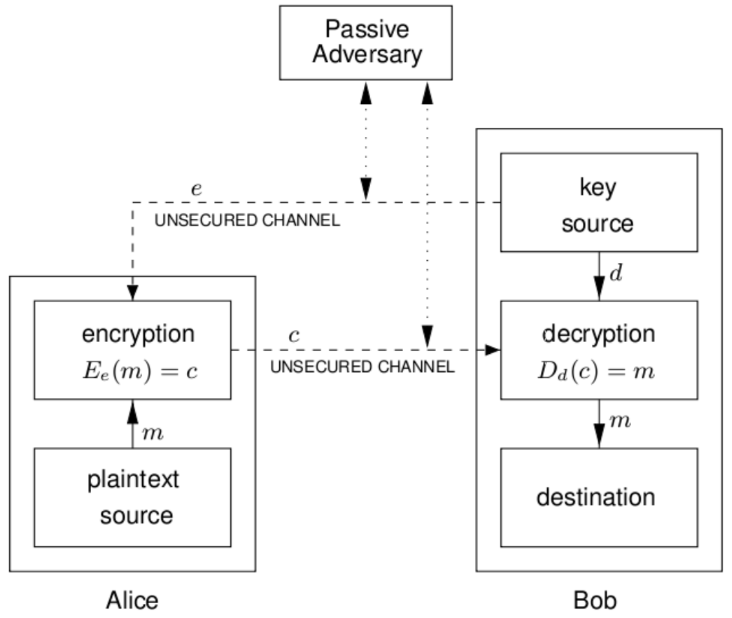
• Attack: Man-in-the-middle attack (MITM)
  • Substitute different public keys between two users
  • Adversary: $(e', d')$
  • All public key systems are vulnerable to MITM, must use authentic public keys.

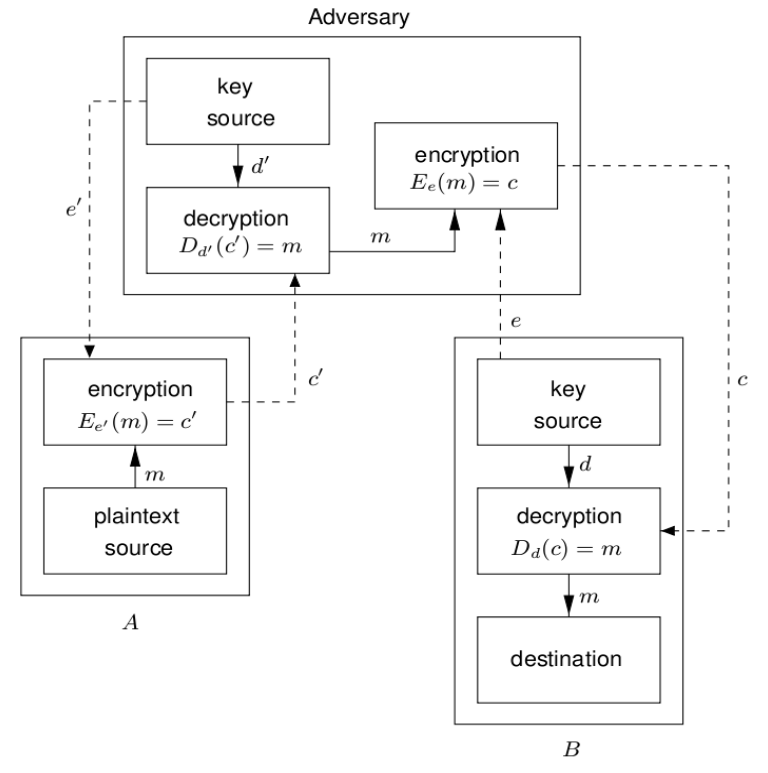
7.4 Public Key Signatures

• Signatures are for integrity and authentication of a message.
• Alice uses her private key $K_{d,Alice}$ to sign $M$ to produce $Sign_{Alice}(M)$.
• Bob uses Alice's public key $K_{e,Alice}$ to verify $Sign_{Alice}(M)$.
• Typical usage mode:
  • Practically, the entire message is not encrypted with a public key, or signed with a private key
    • Reason: Computational expense
  • Encryption: encrypt a symmetric key using the public key, then the message encrypted with the symmetric key.
  • Signature: sign $H(M)$ instead of $M$.

7.5 Diffie-Hellman Key Exchange (D-H Key Exchange)

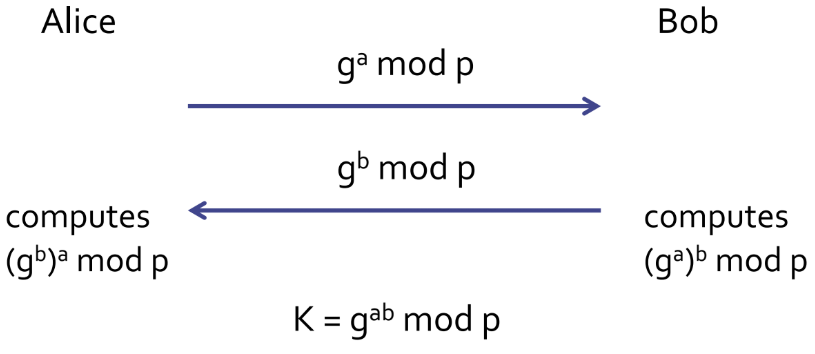
• Overview
  • Enables two parties to jointly establish a shared secret key, no prior shared secret
  • Based on exponentiation in a finite field (modulo a prime)
  • Weakness: no authentication
  • Security relies on the difficulty of computing discrete logarithms (similar to factoring)
• How it works
  • $p$, a large prime integer, public
  • $g$, a primitive root mod $p$, public (also called a generator)
  • Session key is then obtained by both parties calculating:
    • $a,b$ are private to Alice and Bob respectively
    • $K_{ab}=g^{ab}\pmod p$
    • Alice can compute $K_{ab}={g^{b}}^a\pmod p$
    • Bob can compute $K_{ab}={g^{a}}^b\pmod p$
  • $\\\{Message, Password\\\}_k$
• Attack
  • The attacker needs either $a$ or $b$ to compute $K_{ab}$.
  • Or Man in the Middle

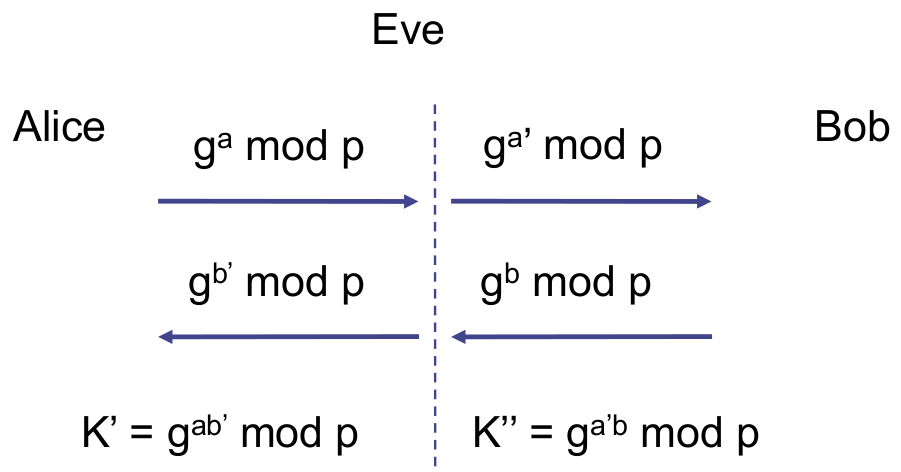
• D-H Man in the Middle
  • Why it works? No authentication
  • How it works?
    1. Alice sent $g^a$, Eve sent $g^{a'}$, Bod received $g^{a'}$
    2. Bob sent $g^b$, Eve sent $g^{b'}$, Alice received $g^{b'}$
  • How it can be solved?
    • Sign the $g^a$ and $g^b$ because the sign key is private.
    • But have to share the key, leads to new problem

7.6 Password Authenticated Key Exchange

• Definition

  • Two parties share only a weak/low-entropy secret, e.g., a password
  • Establish a secure channel between the users using only the shared secret and mutual authentication
  • The channel must be protected by a high-entropy session key
  • Offline guessing attacks on the weak secret must be infeasible

• But how to derive a high-entropy secret from a low entropy one?

• Example

  • Password: 8 bits
  • Generation: sha256(password) generates 256 bits to be used as a key
  • But no need to guess $2^{256}$
  • Still only guess $2^{8}$, then use sha256 to generate a key to test (need a testable sample)

• Authenticated Diffie-Hellman (DH encrypted key exchange)

• Shared passwod

  • $A\rightarrow B: A,g,p,\{g^a \pmod p \}_{pwd}$
  • $B\rightarrow A: B,\{g^b \pmod p \}_{pwd}$
  • $A\rightarrow B: \{C_A\}_K$
  • $B\rightarrow A: \{C_A, C_B\}_K$
  • $A\rightarrow B: \{C_B\}_K$

• Achieves:

  • Mutual authentication
  • Strong session key
  • No offline attacks on PWD
  • Key confirmation

7.7 RSA

• Theory
  • Based on intractability of the integer factor factorization problem
• Key generation
  1. Generate 2 large and distinct primes $p$ and $q$, each roughly the same size.
     • What if one number is not large? (Then, would be too easy to find the other number)
  2. Compute $n=pq$ and $\Phi(n)=(p-1)(q-1)$.
     • $\Phi(n)$ is a relative prime to $n$.
       • e.g.: $\Phi(5\times 7)=4\times 6 = 24$
  3. Select a random integer $e: 1< e < \Phi(n) $
     • gcd$(e,\Phi(n))=1$
     • $e$ can be small for encryption efficiency.
  4. Use extended Euclidean algorithm (HAC) to computer the unique integer $d,1< d <\Phi(n)$, such that $ed\equiv1\pmod{\Phi(n)}$.
  5. Keys
     • Public key is $(e,n)$.
     • Private key is $d$.

7.8 RSA Encryption

• How it works
  • Bob encryption
    1. Get Alice's authentic public key $(e,n)$
    2. Take the message $M$ and represent it as an integer $m$ in the interval $[0, n-1]$.
       • If $M$ cannot be represented in $[0, n-1]$, separate $M$ into blocks.
    3. Computer $c=m^e\pmod n$.
    4. Send $c$ to Alice.
  • Alice decryption
    1. Compute $m=c^d\pmod n$.
• Why it works
  1. Since $ed\equiv1\pmod{\Phi(n)}$, there exists an integer $k$ such that $ed\equiv1+k\cdot \Phi(n)$
  2. $c^d=m^{ed}=m^{1+k\cdot \Phi(n)}=m^1\cdot m^{k\cdot \Phi(n)}=m^1\cdot (m^{\Phi(n)})^k=m^1\cdot (1)^k=m$
     • Euler's theorem: $m^{\Phi(n)}\pmod n =1$ where $gcd(\Phi(n),n)=1$

7.9 Digital Signature

• Scheme:
  • a secret signing key and a public verfication key
• Service provided:
  • Authentication
  • Data integrity
  • Non-Repudiation (MAC does not provide this)
    • $\text{HMAC}_k(M)$, ?
    • $\text{Sign}_A(M)$, because the private key is from the signer
• Problem
  • How do we obtain someone's public key over a network, in a way that we can trust it belongs to the claimed entity?
  • Certificates
    • Relies on a set of trusted third-party certificate authorities to establish the authenticity of certificates.
    • Source is normally a trusted third party (also called: certificate authority (CA)).
    • Root certificates are self-signed.
• Categories
  • With appendix: the signature $s$ of the message $M$ is usually appended to the unmodified message $M$. So $(M,s)$ or $M\|\|s$ is sent.
  • With message recovery: all or some of the message is embedded in the signature. When all of the message is embedded, the verification procedure requires only $s=Sign(M,PrivateKey)$ as input, and recovers $M$ as a by-product (that's known as total message recovery). Only the signature is sent; it embeds the message.

7.10 RSA Signature

• Overview
  • $R$: a redundancy function, maps message $M$ to RSA inputs.
  • No confidentiality: anyone with Alice's public key can recover the message $M$.
  • Authentication and integrity guarantees: only the holder of Alice's private key can create a valid mesage that has a signature verifiable with her public key.
• How it works
  • Alice wants to sign a message $M$:
    • Computes $M'=R(M)$.
    • Computes $s={(M')}^d \pmod n$.
    • Alice's signature for $M$ is $s$.
  • Bob wants to verifty:
    • Obtains Alice's public key $(e,n)$.
    • Computes $M'=s^e \pmod n$.
    • Verifies that $M'$ is in the redundancy space.
    • Recovers $M=R^{-1}(M')$.
• RSA signature with Appendix
  • Alice calculates $h(M)$.
  • Alice signs $s=Sign(h(M))$.
  • Alice transmits $(M,s)$.
  • Bob can verify message by calculating $h(M)$ and comparing $h(M)$ to the verified signautre.
  • PGP (Pretty Good Privacy) uses it to create signautre on email.

7.11 SSL

• Properties
  • What it has
    1. Confidentiality
    2. Message authenticity
    3. Authentication
       • Server authentication
       • Client authentication
  • What it hasn't
    1. Non-repudiation
    2. Availability
• Architecutre
  • between Application layer (HTTP/LDAP/POP3) and Transport layer (TCP)

---

8. Usability and human factors in security

8.1 Pretty Good Privacy (PGP)

• Steps:

  1. Install PGP/GPG/OpenPGP
  2. Generate/import key pairs
  3. Protect your private keys
  4. Integrate/enable in your mail client
  5. Publish your public key
  6. Collect public keys of your contacts

• Encryptoin/Decryption

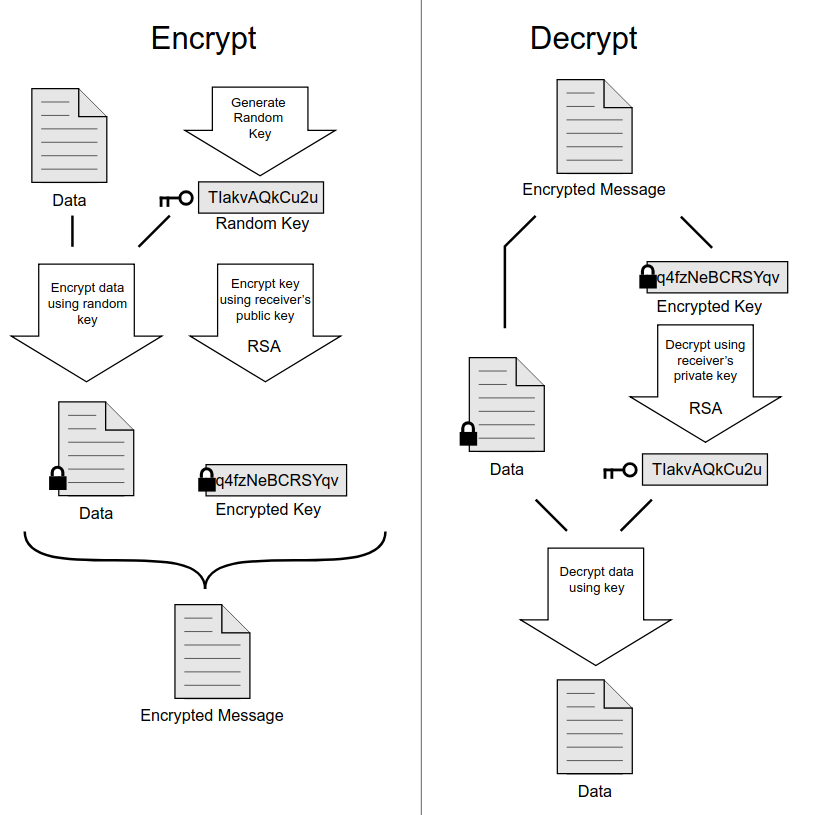
• Why Johnny Can’t Encrypt: A Usability Evaluation of PGP 5.0

  • Hypothesis: effective security requires a different usability standard, and that it will not be achieved through the user interface design techniques
  • Conclusions:
    1. “making security usable will require the development of domain-specific user interface design principles and techniques”
    2. “user interface design for effective security remains an open problem”
  • Usability for security: Security software is usable if the people who are excepted to use it:
    1. are reliably made aware of the security tasks they need to perform;
    2. are able to figure out how to successfully perform those tasks;
    3. don't make dangerous errors; and
    4. are sufficiently comfortable with the interface to continue using it.
  • Problematic properties of security
    1. The unmotivated user property
       • Secondary goal (security is not important)
       • Optimistic view (security is working; nothing to hide)
       • Get help from psychology studies (user capabilities: users cannot remeber long password or users do not know a strong password; how to motivate people)
    2. The abstraction property
       • Policies are abstract
       • Policies vs. implementation
    3. The lack of feedback property
       • How to design effective warning dialogs
       • How to communicate system state
       • Too much feedback can also be bad
    4. The barn door property
       • Once a secret has been left accidentally, even for a short time, it's useless now.
    5. The weakest link property
       • A single user error is enough to defeat a system
       • Users must follow all security guidelines
  • Expected usability standard for PGP
    1. understand encrypt/decrypt
    2. understand authentication
    3. understand generate key pair
    4. understand publish their public key
    5. understand acquire public keys
    6. manage to avoid dangerous errors
    7. be able to succeed at all of the above within a few hours of reasonably motivated effort.
  • PGP's usability evaluation methods
    • Cognitive walkthrough
      • Simulated use by a domain expert
      • Step throug the use of the software
      • Learnability evaluation
    • Cognitive walkthrough: Findings
      • Irreversible actions
        • Accidentally deleting the private key
        • Accidentally publicizing a key
        • Accidentally revoking a key
        • Forgetting the pass phrase (public keys collected from others)
        • Failing to back up the key rings
        • Sending a message to wrong recipients
        • Sending a confidential message as plaintext
        • Failing in signature verfication
        • Failong in revocation check
        • Trusting the wrong keys
      • Consistency of terminologies
        • Encoding vs. encrypting
      • "Too much information"
        • Define what is important and what is not
        • Basic, intermediate, and advanced levels in UI
    • User study
      • Test with real users
    • User study results
      • Dangerous errors
        • 3/12 sent confidential message in plaintext
        • 2 realized the mistake; one did not
        • 1 forgot the passphrase
      • Figuring out how to encrypt with any key
        • 1/12 failed to encrypt at all
        • 2 took close to half an hour
      • Figuring out the correct key to encrypt with
        • 7/11 used their own keys
        • 1 generated key pairs for others
      • Decrypting an email message
        • 2/5 succeeded
      • Deciding whether to trust keys from the key server
        • 3/8 members expressed concern

8.2 Human as an attack vector

• Why
  • Real attacks exploit psychology and technology
  • Phishing, vishing
  • Targeted vs. generic
  • Easy to launch online "imitation" attacks
  • Deception history
• Attacker's goals
  • Information extraction
  • malware infection
    • APT (Advanced persistent threat)
    • Long-term attack vector
  • Stealth
  • monetary gains

8.3 Phishing

• Why
  • Natural trust: attacks via "trusted" contacts
  • Target the vulnerables: elderly, young-adults, low-income
  • Fit with natural work-flow
    • How to detect phishing emails when banks also send similar emalis
  • Greed
  • Social validation
• Phishing user study
  1. Good phishing websites fooled 90% of participants.
  2. Existing anti-phishing browsing cues are ineffective.
  3. On average, the participant group made mistakes on the test set 40$ of the time.
  4. Popup warnings about fraudulent certificates were ineffective.
  5. Neither education, age, sex, previous experience, nor hours of computer use showed a statistically significant correlation with vulnerability to phishing.
• Analysis of past attacks
  1. Victims' lack of knowledge
  2. Visual deception
  3. Bounded attention
     • Too many indicators for different types of security issues

8.4 The RSA SecureId Hack (Hardware authentication token)

• What it is
  • Hardware authentication token
  • Dynamic code
• Use of RSA SecurID
  • Second factor
  • Side notes: three factors of authentication
    • Something you know, have, are
• Issue
  • Auth servers must be in sync and hall all seeds
• Biometrics authentication
  • Once compormised, it cannot be replaced.

8.5 Deception

• What it is
  • Planned actions to mislead attackers and
  • To cause them to:
    • Confuse
    • Take/avoid specific actions
  • Must be mixed with some “truth”
  • Attackers must be given “hope”
• Advantages
  • False info can reduce value of leaked databases
  • Learning the attacker’s moves
  • Slow down the attacker

---

9. Botnets and DDoS

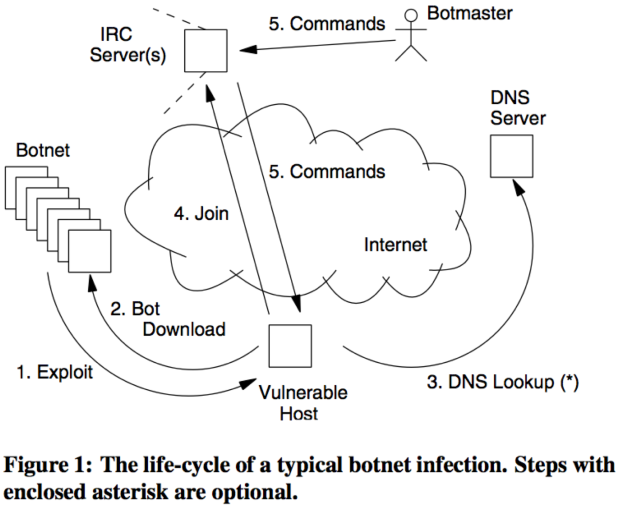
9.1 Botnets

• What it is

  • Bot v.s. malware
    • Bot is controlled by someone remotely
    • malware not
  • Botnets: networks of infected end-hosts, called bots, that are under the control of a human operator commonly known as a botmaster.
  • Bot software: advanced malware that makes the funcationality of a compromised host available to the botmaste.

• Features

  • propagate like worms
  • hide from detection like many viruses
  • attack like many stand-alone tools
  • have an integrated command and control system

• How to infect

  • "curious George" attacks
  • Backdoors from a previous infection
  • Trojaned applications
  • OS/browser/application vulnerabilities
  • Open file shares
  • P2P networks

• How to control:

  • Centralized

    * Better control

    * Efficient attacks

    * Single-point vulnerability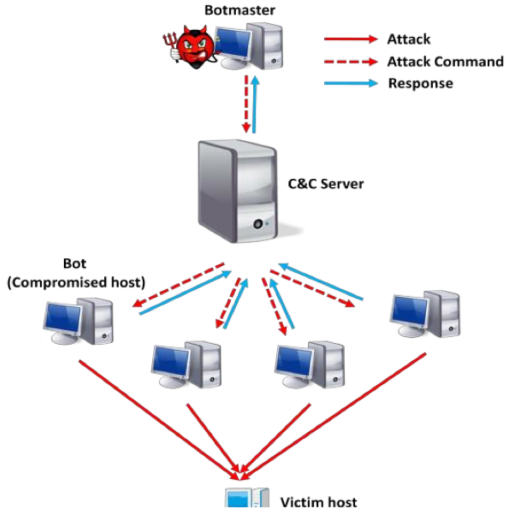

    

  • P2P

    * robust againt disruption

    * Inefficient

    * unreliable from attackers' viewpoint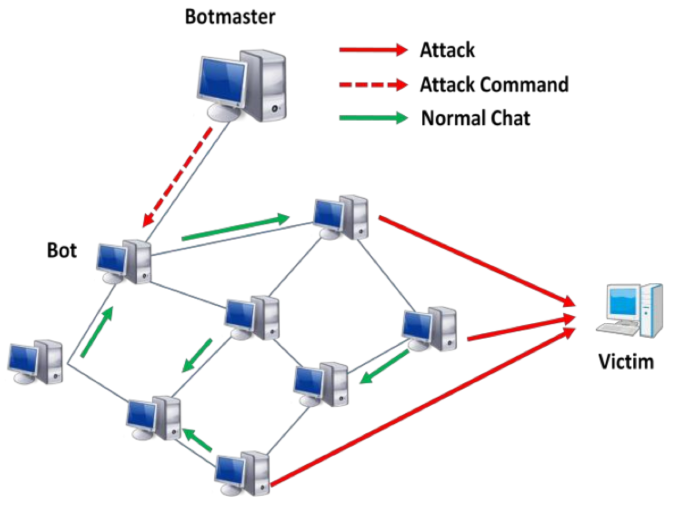

    

  • Hybrid: mixture of centralized and P2P

• How to protect masterbot: Dynamic domain names

  • A single domain is problematic
  • Multiple domains do not help
    • Names can be learned in advanced and blocked
    • Bots can be reverse-engineered to extract domains
  • Domain Generation Algorithms (DGA)
    • Generate domain names depending on one or more external information sources serving predictable seed values that can be accessed by bots and botmasters.
    • Seed values: timestamp, Twitter trends

• Detection

  • Passive techniques
  • Active techniques
    • Sinkholing: Redirecting or dropping traffic destined to a C&C server, malware distribution server or attack server.
  • Reverse engineering of bots

9.2 DDos attacks

• DDos can:
  • Degrades a resource used by a victim (legitimate user) or
  • Denies use of a resource by a victim
  • Clog/crash a resource
• Target resources:
  • network bandwidth,
  • CPU,
  • database/disk bandwidth

9.3 DDos Attack methods

• SYN floods

  • When TCP establishs a connection, it would handshake first:
    • TCP three-way handshake: SYN, SYN-ACK, ACK
    • Half-open connections: SYN, SYN-ACK
  • Weak point
    • Each SYN packet (new connection) mandates the server to allocate resources
  • Attack
    • Attack on the memory
    • Fake/genuine IP addresses can be used to sent tons of SYN packets

• Application-based attacks

  • HTTP flood
    • Generally launched from a botnet (need genuine IP, because have to establish the connection first)
    • Attack
      • Attack on the bandwidth and CPU
      • Large files requests
      • Search service of a site
      • Complex queries

• DNS amplification attack

  • How it works

    1. Compromise an authoritative DNS server and publish a large TXT record

       • TXT record: a type of resource record in the Domain Name System (DNS) used to provide the ability to associate arbitrary text with a host or other name, such as human readable information about a server, network, data center, or other accounting information.

         example.com IN TXT "This domain name is reserved for use in documentation"

    2. The attacker uses botnet to send UDP packets with spoofed IP addresses to a DNS recursor. The spoofed address on the packets points to the real IP address of the victim.

    3. Each one of the UDP packets makes a request to a DNS resolver, often passing an argument such as “ANY” in order to receive the largest response possible.

    4. After receiving the requests, the DNS resolver, which is trying to be helpful by responding, sends a large response to the spoofed IP address.

    5. The IP address of the target receives the response and the surrounding network infrastructure becomes overwhelmed with the deluge of traffic, resulting in a denial-of-service.

  • Difficult to prevent

    • Millions of open recursive DNS servers
    • High capacity servers ("fat" bandwidth)
    • DNS servers are not directly affected – no incentive to adopt known "good practices"
    • may not need to compromise an authoritative DNS server

9.4 Mirai attack

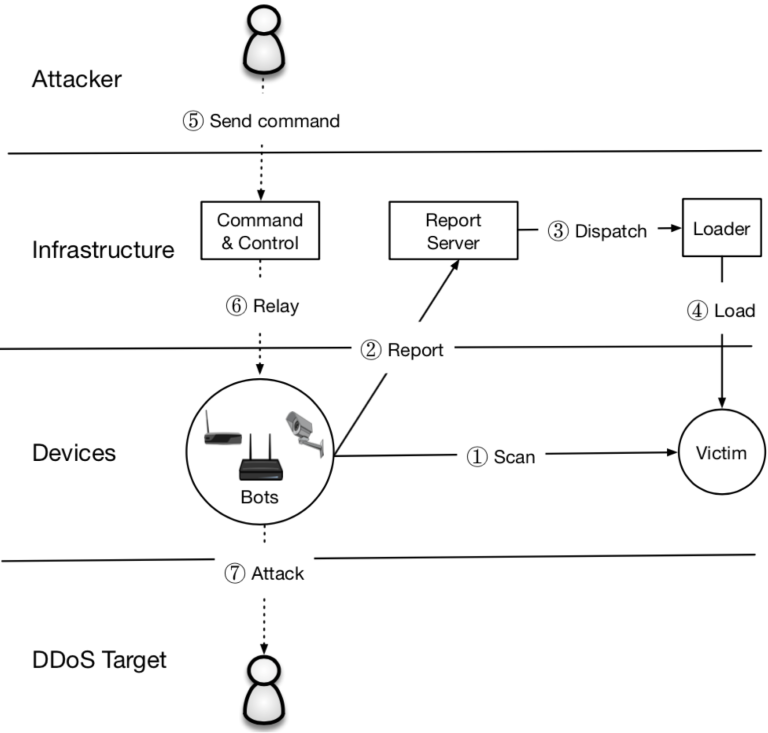
1. Scan: sent TCP CYN probes to pseudorandom IPv4 addresses, excluding blacklist.
   • Why scan? and scan efficient?
     • Stateless: no memeory allocation. But if recevied any response from any device, that device is a potential victim.
2. If a potential victim is found, starts a brute-force login phase.
   • Use preconfigured dictionary, because resource is constrained.
3. Send the victim's IP and associated credentials to Report Server.
4. Report Server dispatches the command to Loader.
5. Loader will try to login the victim devicem then try to find out what kind of this device is.
6. Loader will send corresponding binary to the victim, and the victime would join the botnet.
7. Finally, the attacker would use the botnet to launch other attacks.

---

13. Domain Fronting

What

• Circumvents Internet censorship by obfuscating the domain of a HTTPS connection
• Allows a user to connect to a blocked service (via DNS, IP or deep packet inspection)
• uses different domain names at different layers of communication
• In an HTTPS request, the destination domain name appears in
  • the DNS query,
  • the TLS Server Name Indication (SNI) extension,
  • and the HTTP Host header
• For
  • regular connections, the same domain name is used.
  • domain-fonted connections, HTTP Host has the true destination domain.

Techniques

1. With a front domain name:
2. Domainless fronting

---

14. Write Protection Against Privileged Data Tampering

14.1 Legacy solutions

1. detection via anti-malware
2. key recovery via reverse engineering
3. backup

14.2 Academic proposals

1. monitoring file I/O activities
2. recording encryption keys
3. shadowing file writes

14.3 FlashGuard

• relies on intrinsic properties of SSD writes
• cannot deal with data destruction malware

14.4 Data loss prevention

• Trusted environments
  • TEE-Disk: Self-encrypting devices
    1. Fine-granined access control
    2. programmable control (lock-unlock)
  • TEE-Host: Intel TXT or AMD SVM
    1. Dynamic root of trust, measured, isolated
    2. Sealed secret (platform state binding)
    3. Device I/O access
• Design
  • Stand-alone: occasional interruptions due to TXT exclusiveness
  • Network-based: any user device, no interruptions
• Space cleanup
  • Automatic stale version deletion
  • Mini file browser: manual file deletion (within the trusted updater)
• Challenges
  1. Safely use I/O devices from the user OS
  2. Programming the SED OPAL interface
  3. DMA access in TEE
  4. Porting Flicker to Windows 10 64-bit
  5. Security
     1. Outside the trusted environment, can malware update files on the protected partition?
     2. Inside the trusted environment, can malware trick the updater to write arbitrary content?
• Attacks to consider
  • Forged UI
  • Termination
  • Flaws in TEE implementations
  • Persistent attacker (delayed attacks after deletion)

---

Tutorial 9 - RSA/AES encryption with OpenSSL

Public key crypto

Release your public key

Usage:

• Encryption

1. Anyone encrypts using your public key
2. Nobody can decrpty but you with your private key

• Signature

1. You sign some data with your private key
2. Anyone can verify your signature with your public key

RSA encryption/decryption with OpenSSL

Generate key

openssl genrsa -aes256 -out alice.key 2048

Steps

1. Extract the public key

openssl rsa -in alice.key -pubout -out alice.pub

2. (Optional) look at Alice's public key

openssl rsa -in alice.pub -pubin -noout -text

2. Pass the public key to Bob
3. Bob encrypt the message with Alice's public key

openssl rsautl -encrypt -inkey alice.pub -pubin -in secret.txt -out secret.txt.enc

4. Bob pass the encrypted message to Alice
5. Alice decrypt the message with her private key

openssl rsautl -decrypt -inkey alice.key -in secret.txt.enc -out secret.txt.dec

Problem

1. Computation expensive
2. Plaintext's size should be smaller than the modulus (2048)

Solution

• Hybrid encryption: Asymmetric and symmetric encryption
• RSA encrypt a symmetric key to encrypt secret

AES encryption/decryption with OpenSSL

Steps

1. Bob generates a random AES key and IV:

openssl rand -hex -out aes.key 32

openssl rand -hex -out aes.iv 16

• 32$=256$ bits (key size for AES-256)
• 16$=128$ bits (block size for AES-256)

2. Bob encrypts the message with his own AES key and IV

openssl enc -aes-256-cbc -in secret.txt -out secret.txt.enc -K %key% -iv %iv% -p

3. Bob encrypts the AES key and IV with Alice's public key

openssl rsautl -encrypt -inkey alice.pub -pubin -in aes.key -out aes.key.enc

openssl rsautl -encrypt -inkey alice.pub -pubin -in aes.iv -out aes.iv.enc

4. Bob send aes.key.enc, aes.iv.enc, secret.txt.enc to Alice
5. Alice decrypts the AES key and IV

openssl rsautl -decrypt -inkey alice.key -in aes.key.enc -out aes.key.dec

openssl rsautl -decrypt -inkey alice.key -in aes.iv.enc -out aes.iv.dec

6. Alice decrypts the encrypted message

openssl enc -d -aes-256-cbc -in secret.txt.enc -out secret.txt.dec -K

%key% -iv %iv%

Alternative Steps

• Use PBKDF2 to simplify key and IV generation

1. Bob eenerate a password randomly

openssl rand -hex -out pass.key 32

2. Bob encrypts using a file as password

openssl enc -aes-256-cbc -in secret.txt -out secret.txt.enc -pass file:pass.key -pbkdf2 -iter 100000 -md sha256

3. Bob encrypts the password file with Alice's public key

openssl rsautl -encrypt -inkey alice.pub -pubin -in pass.key -out pass.key.enc

4. Bob send pass.key.enc, secret.txt.enc to Alice
5. Alice decrypts the password file

openssl rsautl -decrypt -inkey alice.key -in pass.key.enc -out pass.key.dec

6. Alice decrypts the secret using the password file

openssl enc -d -aes-256-cbc -in secret.txt.enc -out secret.txt.dec -pass

file:pass.key.dec -pbkdf2 -iter 100000 -md sha256